The Building Blocks of Neural Networks
Neural networks might seem like a big, scary idea, but in this second post of this series, we’re breaking them down into bite-sized pieces! Imagine it’s like building with colorful blocks!

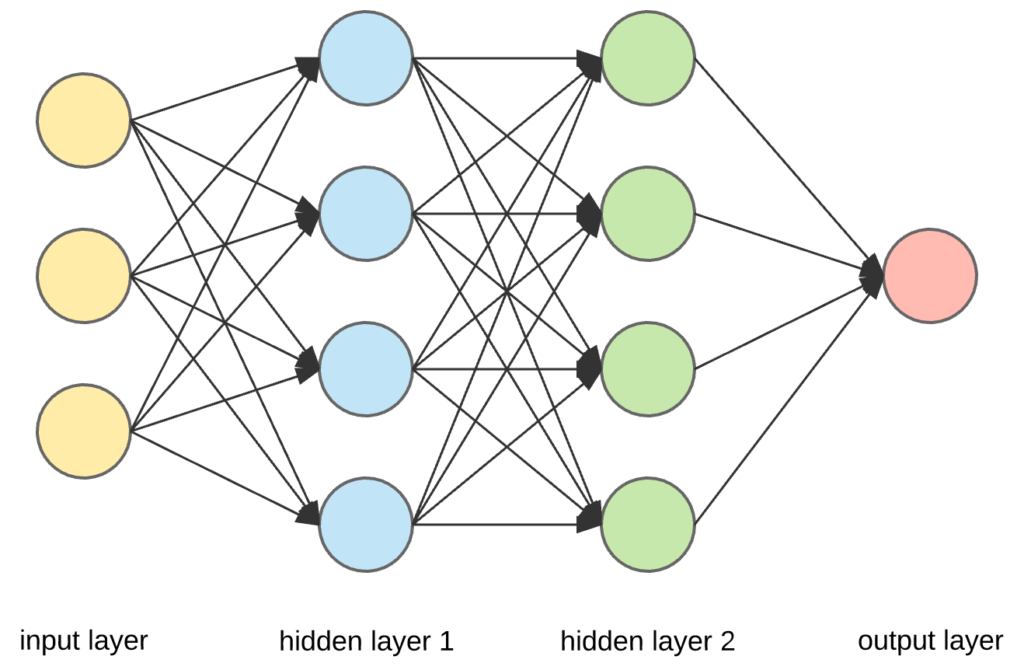
Explore the layers in a neural network: input, hidden, and output
Imagine a neural network like a sandwich-making robot!

- Input Layer: This is where we show the robot our ingredients, like bread and fillings. It’s the first stop where data enters the network. It’s where we give our network data to munch on. It’s where we introduce our data to the network. Think of it as the foundation of our structure, where information enters.
- Hidden Layers: These are like the robot’s secret kitchen. They process the ingredients in a special way, making the sandwich taste just right! The “hidden” layers do secret stuff in between, like solving puzzles. These layers process and learn from the data. They uncover patterns and details that might not be obvious at first glance.
We can have 0 or more hidden layers, and each hidden layer takes inputs from the previous layer. - Output Layer: Here, the robot serves us the final sandwich. It’s what we wanted all along! the “output” layer gives us the answer.
This is the end result, our network’s way of expressing what it’s learned. It could be an answer to a question or a classification of data.
Understand the Purpose of Activation Functions
Activation functions are like the chef’s special spices! They are used in the hidden layers.
- Without Activation: Our robot might make bland sandwiches, never too spicy or too mild.
- With Activation: Now, our chef (the neural network) can add just the right amount of spice to make the sandwich taste amazing!
Activation functions are like buttons in our network. Activation functions are like the glue that holds our blocks together. They decide if a neuron (a tiny decision-maker in the network) should get excited or stay calm, should fire up or stay quiet.
One common button is ReLU, which says, “If you’re positive, be happy; if you’re negative, stay quiet.”, Other functions like Sigmoid, and Tanh help the network make sense of complex data.It helps our network learn better!
Let’s see a simple Python example:
# Imagine we're making a sandwich with two ingredients (input layer) bread = 2 # Bread slices filling = 3 # Fillings (cheese, lettuce, etc.) # Hidden layer - adding them up and doubling the taste! hidden_layer = (bread + filling) * 2 # activation function# Output layer - serving our delicious sandwich! output_layer = hidden_layer print("Our tasty sandwich has", output_layer, "layers!")
In this fun example, we used Python to show how the input layer (bread and filling) goes through the hidden layer, valuate the inputs, apply a function to them, and gets served in the output layer. Activation functions add that extra flavor!
Question 1: What role does the Input Layer play in a neural network?
A) It serves the final output.
B) It processes data like a secret kitchen.
C) It’s where data enters the network.
D) It adds flavor to the output.
Question 2: What is the purpose of Hidden Layers in a neural network?
A) They serve as the final output.
B) They process data like a secret kitchen.
C) They add extra spice to the robot’s cooking.
D) They let data enter the network.
Question 3: In the context of activation functions, what happens when you don’t use them in a neural network?
A) The robot makes bland sandwiches.
B) The robot serves amazing sandwiches.
C) The robot becomes too smart.
D) The robot becomes too slow.
Question 4: How do activation functions affect the output of a neural network?
A) They make the output extremely spicy.
B) They have no impact on the output.
C) They add just the right amount of “flavor” to the output.
D) They double the output.
Question 5: What is the main purpose of activation functions in a neural network?
A) To make the network run faster.
B) To make the output extremely bland.
C) To add the right amount of flavor to the output.
D) To remove all flavor from the output.
1C – 2B – 3A – 4C – 5C
